L’analisi di regressione multipla è una tecnica di analisi statistica multivariata che ha lo scopo di determinare il rapporto tra tra una variabile considerata come “obiettivo” della ricerca (variabile dipendente) e un insieme di variabili esplicative (o variabili indipendenti).
In termini pratici tale tecnica viene utilizzata per prevedere una serie di dati temporali futuri al fine di addivenire delle ipotesi o delle relazioni di dipendenza anche attraverso l’uso della statistica inferenziale.
Nel caso in cui la relazione esistente tra le variabili in gioco fosse conosciuta con esattezza si potrebbe perfettamente definire la risposta della variabile dipendente alle sollecitazioni delle variabili esplicative, ma tale caso accade di rado soprattutto nella realtà economica. Si ha infatti che raramente si conoscono tutte le variabili esplicative rilevanti; inoltre alcune di tali variabili possono non essere misurabili o sono misurabili solo con errore; ancora può non essere nota la forma funzionale della relazione. In altre parole, empiricamente la relazione fra variabile dipendente e variabili esplicative può essere conosciuta a meno di un errore; per tener conto di tali condizioni, occorre utilizzare modelli probabilistici: uno di questi modelli è appunto il modello di regressione multipla. Ecco quindi che un manager può essere interessato a conoscere come le vendite di un particolare prodotto sono relazionate al suo prezzo, al prezzo dei prodotti concorrenti, all’ammontare delle spese di pubblicità e di promozione operate dalla propria azienda e dalle altre azienda del settore o, in ambito macroeconomico, un economista può essere interessato a valutare l’elasticità del Prodotto Interno Lordo al variare della spesa pubblica o degli investimenti del settore privato. Si ha che la serie di dati temporali relativi al prezzo di un prodotto o all’elasticità del PIL che rappresentano le variabili obbiettivo, sono la risultante di un cluster di variabili esplicative quali i prezzi offerti dalla concorrenza o le spese di pubblicità nel primo caso, la spesa pubblica o investimenti privati nel secondo caso.
Ciò premesso l’obbiettivo di questo articolo, è quello di descrivere in concreto un esempio di applicazione del modello di regressione multipla, tratterò l’analisi dei passeggeri trasportati da un compagnia aerea in una tratta della durata di circa 1 ora di volo. Ho pensato di utilizzare un caso relativo al settore in cui lavoro proprio perché testato da me nella pratica, ergo all’interno degli accadimenti aziendali. Eviterò in questa sede di citare il nome della compagnia aerea che identificheremo con Y e gli aeroporti di decollo e atterraggio della tratta oggetto di analisi che identificheremo con A e B.
Business Case:
Distribuzione della variabile quantitativa dipendente
Il numero di pax trasportati dalla compagnia aerea Y sulla tratta da A a B negli anni 2011 e 2012 è la variabile dipendete della presente analisi.
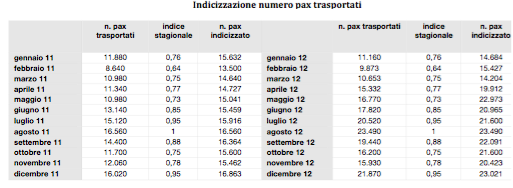
Occorre precisare che il numero dei passeggeri è indicizzato, al fine di sterilizzare il dato dell’effetto stagionalità che ha notevole rilevanza nel modello di business del trasporto aereo. Più nello specifico, si sono utilizzati gli indici standard pubblicati dalla IATA, (International Air Trasport Association), al fine di mediare i flussi di traffico attraverso i mesi dell’anno secondo lo schema riportato nel modello sottostante.
La distribuzione della variabile, appare alquanto equilibrata, non vi sono outliers.
La mediana tende verso il 1° quartile, e la stessa sfiora il limite inferiore dell’intervallo di confidenza, ciò denota una marcata differenza tra media e mediana.
La differenza interquartile tende verso le osservazioni situate sul wafer inferiore.
Distribuzione delle variabili quantitative indipendenti
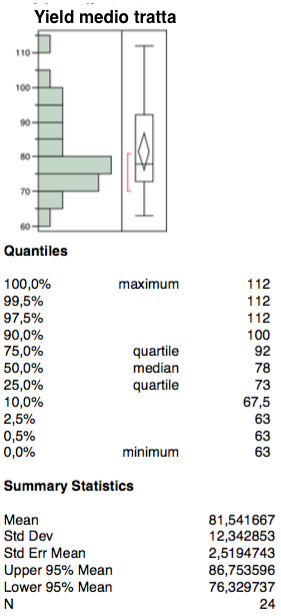 La prima variabile indipendente è rappresentata dallo yield medio, ovvero il ricavo al netto delle tasse per passeggero trasportato. Esso è influenzato dal riempimento dell’aeromobile, si ha che all’aumentare delle vendite, vengono ad essere chiuse le classi a prezzo inferiore per lasciar spazio a quelle a tariffa maggiore.
La prima variabile indipendente è rappresentata dallo yield medio, ovvero il ricavo al netto delle tasse per passeggero trasportato. Esso è influenzato dal riempimento dell’aeromobile, si ha che all’aumentare delle vendite, vengono ad essere chiuse le classi a prezzo inferiore per lasciar spazio a quelle a tariffa maggiore.
La distribuzione della variabile presenta un whole tra i valori 105 e 110 per come è evidente nel grafico relativo all’analisi bivariata rispetto alla variabile dipendente. Dal grafico di correlazione non sono presenti fenomeni di distribuzione bi-modale (paradosso di Simpson) ne outliers.
L’intervallo interquartile tende verso il wafer inferiore; l’intervallo di confidenza appare abbastanza centrato rispetto all’intervallo interquartile. Infine, la mediana tende verso il primo quartile ben al di sotto della media.
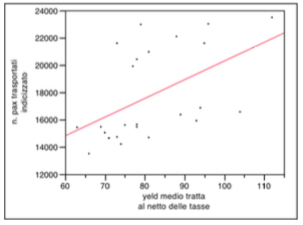
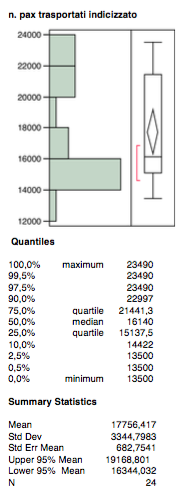
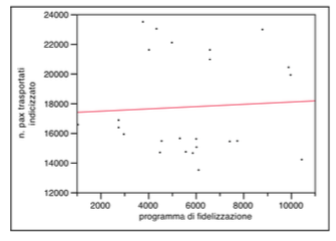
La seconda variabile indipendente riguarda gli investimenti legati al programma di fidelizzazione, ovvero i costi sopportati in relazione alla comunicazione dello stesso e ai biglietti premio concessi ai passeggeri al raggiungimento delle soglie di punteggio previste per il premio.
Anche in questo caso la distribuzione si presenta senza outliers ne vi sono presenti fenomeni di distribuzione bi-modale come è evidenziato dal grafico sottostante dell’analisi bivariata .
Per quanto riguarda la mediana, essa è molto vicino alla media, ergo l’intervallo di confidenza appare molto centrato all’interno dell’intervallo interquartile. A sua volta quest’ultimo appare abbastanza simmetrico rispetto alla distribuzione della variabile.
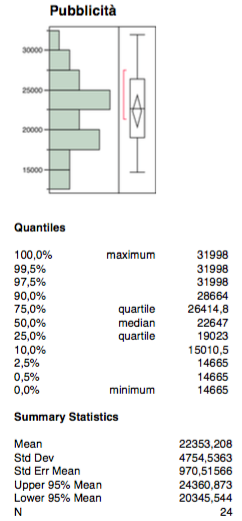
La terza variabile quantitativa indipendente riguarda i costi in comunicazione sui media.
La distribuzione non presenta outliers ne fenomeni bimodali, media e mediana si trovano abbastanza vicini e, sia l’intervallo di confidenza che quello interquartile, sono abbastanza centrati lungo la distribuzione.
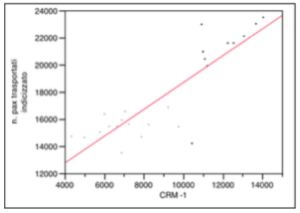
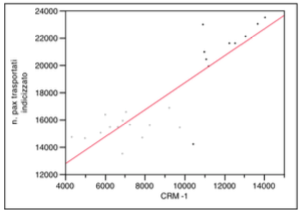
La quarta variabile indipendente CRM -1 è riferita agli investimenti in comunicazione diretta verso il cliente e più in generale ai costi di customer care. Essendo un tipo di investimento non ad effetto immediato, è ragionevole pensare di vederne gli effetti il mese successivo a quando si è operato. Ecco il significato del -1.
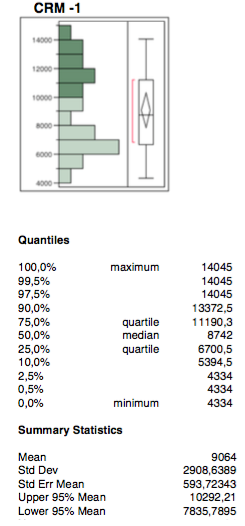
La variabile non presenta outliers ma si notano leggeri fenomeni di distribuzione bimodale dal grafico dell’analisi bivariata. A tal proposito è stata utilizzata la varabile dicotomica “6 frequenza giornaliere” al fine di coniugare le due distribuzioni.
Media e mediana sono abbastanza distanti e, sia l’intervallo interquartile che l’intervallo di confidenza, tendono ai valori inferiori della distribuzione.
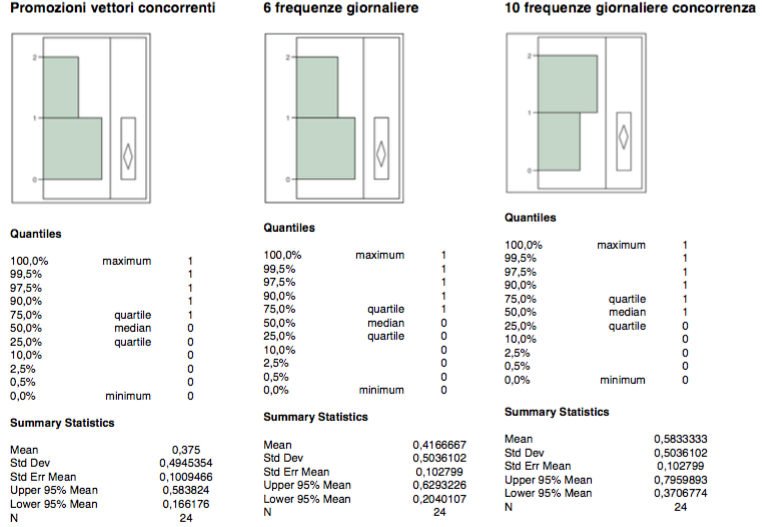
Le variabili dicotomiche si = 1 no = 0 sono connesse:
a) all’esistenza di promozioni in atto di vettori concorrenti sulla tratta;
b) al passaggio a 6 frequenze giornaliere dalle precedenti 4 anche a soluzione del fenomeno di bimodalità presente nella variabile CRM -1
c) al passaggio da parte delle concorrenza da 10 a 8 frequenze giornaliere
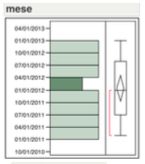
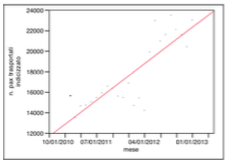
Distribuzione della variabile temporale
Come si evince dal grafico, la relazione tra numero pax trasportati e arco temporale, che ha nei mesi la propria unità di misura, non presenta fenomeni di distribuzione bimodale.
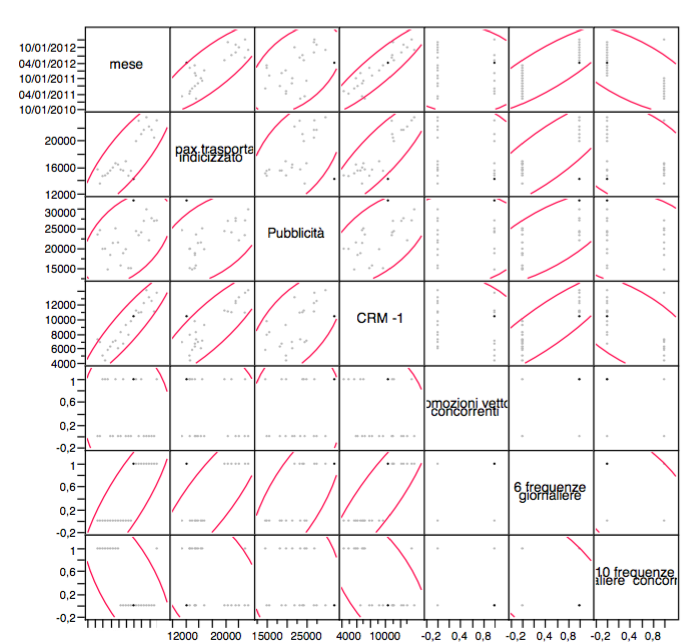
La matrice di correlazione presenta alcuni valori di ρ relativi alle variabili indipendenti abbastanza elevati, questo è anche evidenziato dalla matrice scatterplot. Ergo, è la variabile mese quella con coefficienti di relazione più alti rispetto alle altre variabili indipendenti. A questo punto, onde evitare un aumento artificiale della variabilità spiegata e quindi il fenomeno della multicollinearità si elimina tale variabile, prima dell’analisi locale e globale.
Analisi degli outlyers multivariati
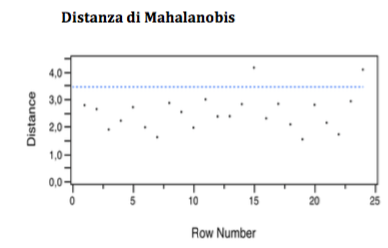
L’analisi eseguita secondo la distanza di Mahalanobis evidenzia una certa costanza della dissimilarità delle osservazioni che rimane pressoché uguale.
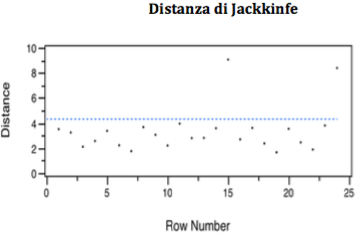
La distanza di Jakknife, in questo caso, conferma sostanzialmente quella di Mahalanobis, ergo vengono ad essere eliminate in quanto outliers: l’osservazione n. 15 e la n. 24.
Analisi globale
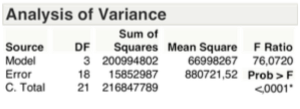
Il valore di R^2, considerando la tabella sotto, dimostra un alto indice di correlazione tra le variabili, peraltro confermato dal valore di R^2 adjusted:
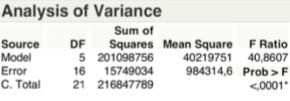
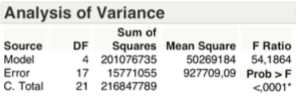
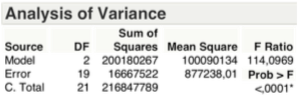
Il Test F o di Durbin – Watson, relativo alla varianza spiegata, come si evince dalla tabella sotto, pone in condizione di rifiutare l’ipotesi Ho con una significatività minore del 1 per mille, ovvero vi è almeno un β diverso da zero.
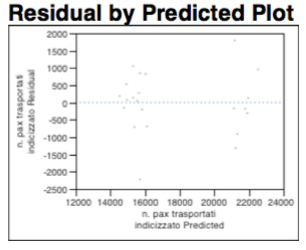
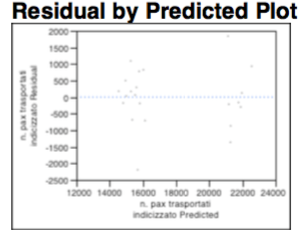
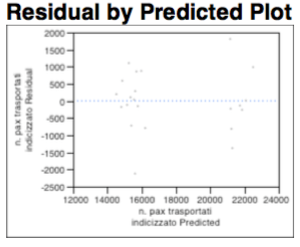
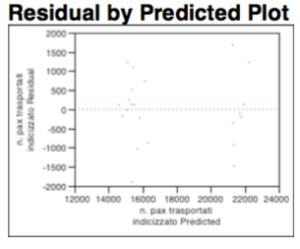
L’analisi dei residui, malgrado il whole spiegato comunque dalla variabile dicotomica relativa alle 6 frequenze giornaliere, rimane comunque una distribuzione dei punti casuale che non implica l’utilizzo di trasformazioni lineari. Non sono presenti fenomeni di eteroschedasticità, e non si riconoscono “forme geometriche note” infine la nuvola appare casualmente popolata, così per come dimostrato nel grafico sottostante:
Analisi locale
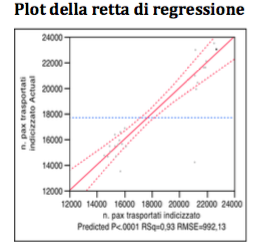
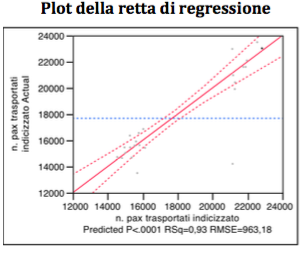
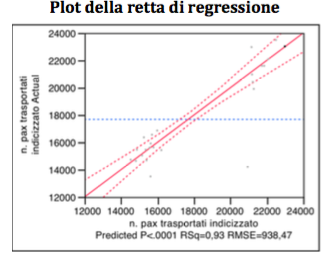
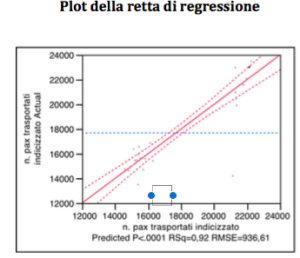
Per come evidenziato anche dal plot della retta di regressione, il VIF > 10 riguarda la variabile CRM -1, il valore di 12,5 consiglia però di non eliminare la variabile. Ergo, secondo il metodo backward, viene ad essere eliminata la variabile: “promozione vettori concorrenti”.
Analisi globale
A seguito dell’eliminazione della variabile “promozione vettori concorrenti”, si evince dal “summary of fit” sottostante, che R^2 diminuisce leggermente, mentre si ha l’aumento del valore di R^2 adjusted.
Il Test F relativo alla varianza spiegata, per come evidenziato dalla tabella sottostante, è superato, ergo si può ancora rifiutare l’ipotesi Ho.
L’analisi del diagramma dei residui denota un consolidamento del whole, continuano a non essere presenti fenomeni di eteroschedasticità o forme geometriche note.
Analisi locale
A seguito dell’eliminazione effettuata, il plot e la tabella sottostante dimostrano che il VIF della variabile CRM -1 è rientrato entro il limite rappresentato dal valore 10, ergo la scelta di non eliminare la variabile si sta rilevando corretta. Si prosegue, sempre secondo l’approccio backward eliminando la variabile “pubblicità”.
Analisi locale
Seguendo l’approccio backward, alla luce del diagramma della retta di regressione e della tabella dei dati stimati per come evidenziati qui di seguito, escludo la variabile: “10 frequenza giornaliere”
Analisi globale
Il “summary of fit” dimostra che il valore di R^2 continua a diminuire, mentre R^2 adjusted, continua ad aumentare.
Il Test F, relativo alla varianza spiegata, come si evince dalla tabella sottostante, pone ancora in condizione di rifiutare l’ipotesi Ho.
Non vi sono sostanziali differenze nel diagramma dei residui.
Analisi locale
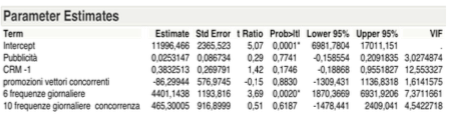
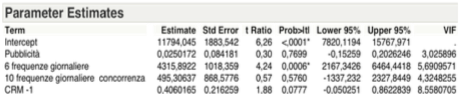
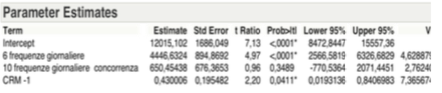
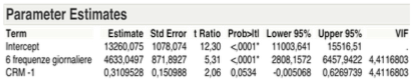
Anche se i parametri stimati dalla tabella sottostante evidenziano un valore leggermente maggiore al livello di significatività pari al 5% della variabile CRM-1, essa può essere considerata esplicativa rispetto alla variabile obbiettivo.
Ergo alla fine dell’analisi locale si ha che le variabili indipendenti rimaste sono:
1) 6 frequenze giornaliere = X1
2) CRM-1 = X2
A questo punto del processo di analisi, occorre standardizzare i parametri riferiti alle due variabili rimaste al termine del processo di selezione, ovvero occorre calcolare i relativi Standard β che rispetto ai valori dei parametri stimati, sono numeri puri, ovvero non risentono delle differenti unità di misura o dei differenti valori quantitativi delle variabili e che rappresentano i pesi attribuiti alle variabili indipendenti rimaste, all’interno della funzione relativa alla retta di regressione.
Ergo considerando il valore dell’intercetta pari a 13.260,08 per come evidenziate dall’ultima tabella dei parametri stimati in analisi locale, si ha che il valore standardizzato di X1, ovvero il β1 è pari a 0,709884 mentre il β2 riferito alla variabile X2 è pari a 0,275129. Possiamo a questo punto identificare l’equazione della retta di regressione relativa ai passeggeri trasportati mensilmente sulla tratta da A a B per come segue:
Y = 13.260,08 + 0,7099 X1 + 0,2751 X2
CONCLUSIONI:
L’analisi di regressione condotta con l’approccio backward, definisce le frequenze giornaliere e il Customer Relation Manager le variabili significative in termini di varianza spiegata al fine di prevedere il numero di passeggeri trasportati sulla tratta da A a B.
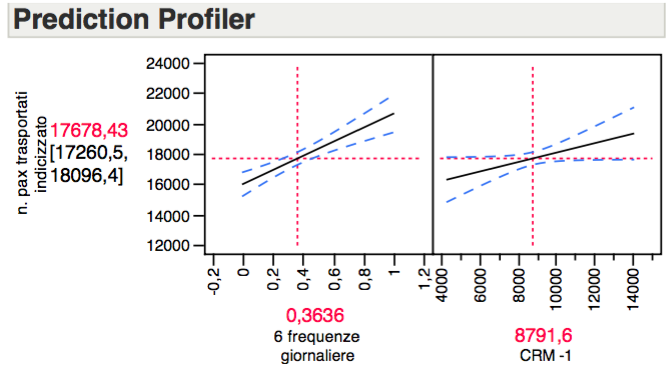
Più nello specifico, si ha che mantenendo costante il numero di frequenze, un aumento dell’investimento in CRM per 1000 € produce il mese successivo un aumento di circa 311 passeggeri su base mensile. Viceversa tenendo costante l’investimento in CRM, l’aumento di una rotazione che equivale a 2 frequenze produce un aumento di circa 4633 passeggeri su base mensile.
L’equazione può essere considerata abbastanza realistica sia rispetto alle variabili, sia rispetto ai pesi attribuite alle stesse.
Di seguito, per concludere, il grafico che mostra l’inclinazione delle due variabili e la loro correlazione rispetto alla variabile dipendente.








Sempre saputo che Intrieri è un titolare di cattedra di ingegneria gestionale di compagnia aerea…
veramente un elaborato eccellente.
Non credo che esistano in circolazione simili prototipi.
Complimenti
Finalmente in Italia qualcosa di nuovo da studiare. OK
Grazie mille Giuseppe.